Baugh-Wooley Multiplier
現在有兩個 signed number $A$, $B$,各有 $n$ 個 bits
$$ A = -a_{n-1} 2^{n-1} + \sum^{n-2}_{i=0} a_i 2^i $$ $$ B = -b_{n-1} 2^{n-1} + \sum^{n-2}_{i=0} b_i 2^i $$做 $A$, $B$ 相乘,可以得到以下式子:
$$ \begin{align} P &= A \times B \\ &= (-a_{n-1} 2^{n-1} + \sum^{n-2}_{i=0} a_i 2^i) \times (-b_{n-1} 2^{n-1} + \sum^{n-2}_{i=0} b_i 2^i) \\ &= a_{n-1} b_{n-1} 2^{2n-2} + \sum^{n-2}_{i=0} \sum^{n-2}_{j=0} a_i b_j 2^{i+j} - 2^{n-1} \sum^{n-2}_{i=0}a_i b_{n-1} 2^i - 2^{n-1} \sum^{n-2}_{j=0}a_{n-1} b_j 2^j \end{align} $$目標是對後兩項的減法做 2’s complement,首先有以下的觀察:
- 後兩項都為 $n-1$ 個 bits
- 後兩項都是由 $2^{n-1}$ 做到 $2^{2n-3}$
- 做乘法的話是要從 $2^0$ 做到 $2^{2n-1}$
我們可以將最後兩項表示成以下形式:
$$ X = -0 \times 2^{2n-1} + 0 \times 2^{2n-2} + 2^{n-1} \sum^{n-2}_{i=0} x_i 2^i + \sum^{n-2}_{j=0} 0 \times 2^j $$也就是 (1) 第 $2n - 1$ 項 (2) 第 $2n - 2$ 項 (3) 第 $n-1$ 到 $2n-3$ 項 (4) 第 $0$ 到 $n-2$ 項
把他展開成 2n 個 bit 來看的話就是:
| 2n - 1 | 2n - 2 | 2n - 3 | 2n -4 | … | n | n - 1 | n - 2 | n - 3 | … | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | $x_{n-2}$ | $x_{n-3}$ | … | $x_1$ | $x_0$ | 0 | 0 | … | 0 |
做 2’s complement 後就是:
| 2n - 1 | 2n - 2 | 2n - 3 | 2n -4 | … | n | n - 1 | n - 2 | n - 3 | … | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | $\overline{x_{n-2}}$ | $\overline{x_{n-3}}$ | … | $\overline{x_1}$ | $\overline{x_0}$ | 1 | 1 | … | 1 + 1 |
化減後就是:
| 2n - 1 | 2n - 2 | 2n - 3 | 2n -4 | … | n | n - 1 | n - 2 | n - 3 | … | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | $\overline{x_{n-2}}$ | $\overline{x_{n-3}}$ | … | $\overline{x_1}$ | $\overline{x_0}$ + 1 | 0 | 0 | … | 0 |
因為後面一共有兩項 2’s complement,所以要加兩次:
| 2n - 1 | 2n - 2 | 2n - 3 | 2n -4 | … | n | n - 1 | n - 2 | n - 3 | … | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | $\overline{x_{n-2}}$ | $\overline{x_{n-3}}$ | … | $\overline{x_1}$ | $\overline{x_0}$ + 1 | 0 | 0 | … | 0 |
| 1 | 1 | $\overline{y_{n-2}}$ | $\overline{y_{n-3}}$ | … | $\overline{y_1}$ | $\overline{y_0}$ + 1 | 0 | 0 | … | 0 |
其中可以看到第 $n - 1$ 位 bit,其實就等於在 $2^n$ 多加 1。
再看到 $2n - 1$ 及 $2n - 2$ 位 bit,其實最終結果就是 $2n - 1$ 位 bit 為 1,$2n - 2$ 位 bit 為 0。
所以實際上要處理的就是這些 bits:
| 2n - 3 | 2n -4 | … | n | n - 1 |
|---|---|---|---|---|
| $\overline{x_{n-2}}$ | $\overline{x_{n-3}}$ | … | $\overline{x_1}$ | $\overline{x_0}$ |
| $\overline{y_{n-2}}$ | $\overline{y_{n-3}}$ | … | $\overline{y_1}$ | $\overline{y_0}$ |
化成式子就是:
$$ 2^{n-1} \sum^{n-2}_{i=0} \overline{a_i b_{n-1}} 2^i + 2^{n-1} \sum^{n-2}_{j=0} \overline{a_{n-1} b_j} 2^j $$最終代回去就可以得到以下式子:
$$ P = a_{n-1} b_{n-1} 2^{2n-2} + \sum^{n-2}_{i=0} \sum^{n-2}_{j=0} a_i b_j 2^{i+j} + 2^{n-1} \sum^{n-2}_{i=0} \overline{a_i b_{n-1}} 2^i + 2^{n-1} \sum^{n-2}_{j=0} \overline{a_{n-1} b_j} 2^j - 2^{2n-1} + 2^n $$硬體
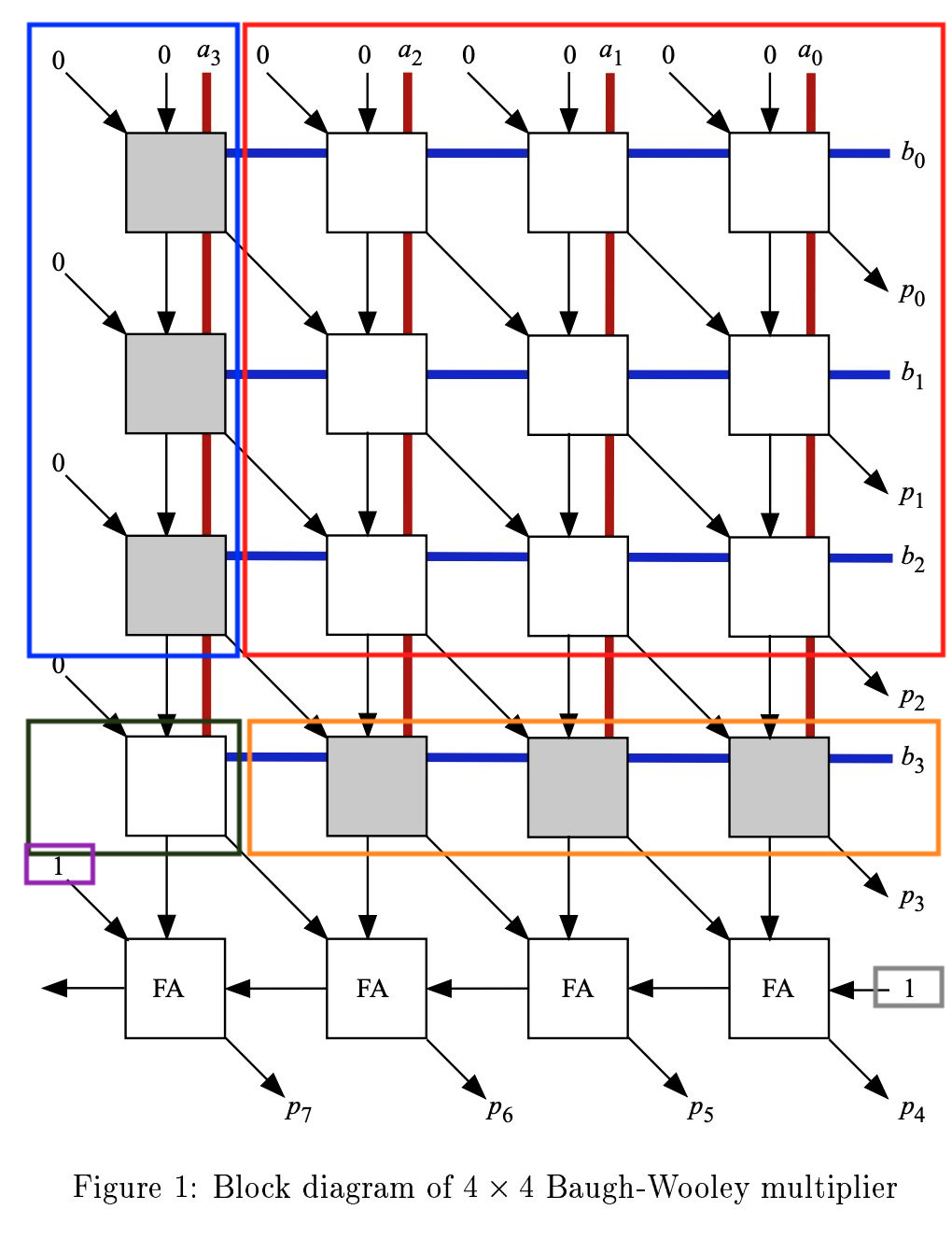
綠色框框是 P 的第一項,紅色框框是 P 的第二項,橘色框框是 P 的第三項,藍色框框是 P 的第四項,紫色框框是 P 的第五項,灰色框框是 P 的第六項。
因為對角線都是相同的 bit 位數,因此可以直接把 carry 往下傳,然後把 adder 算出來的結果往右下對角傳下去累加。
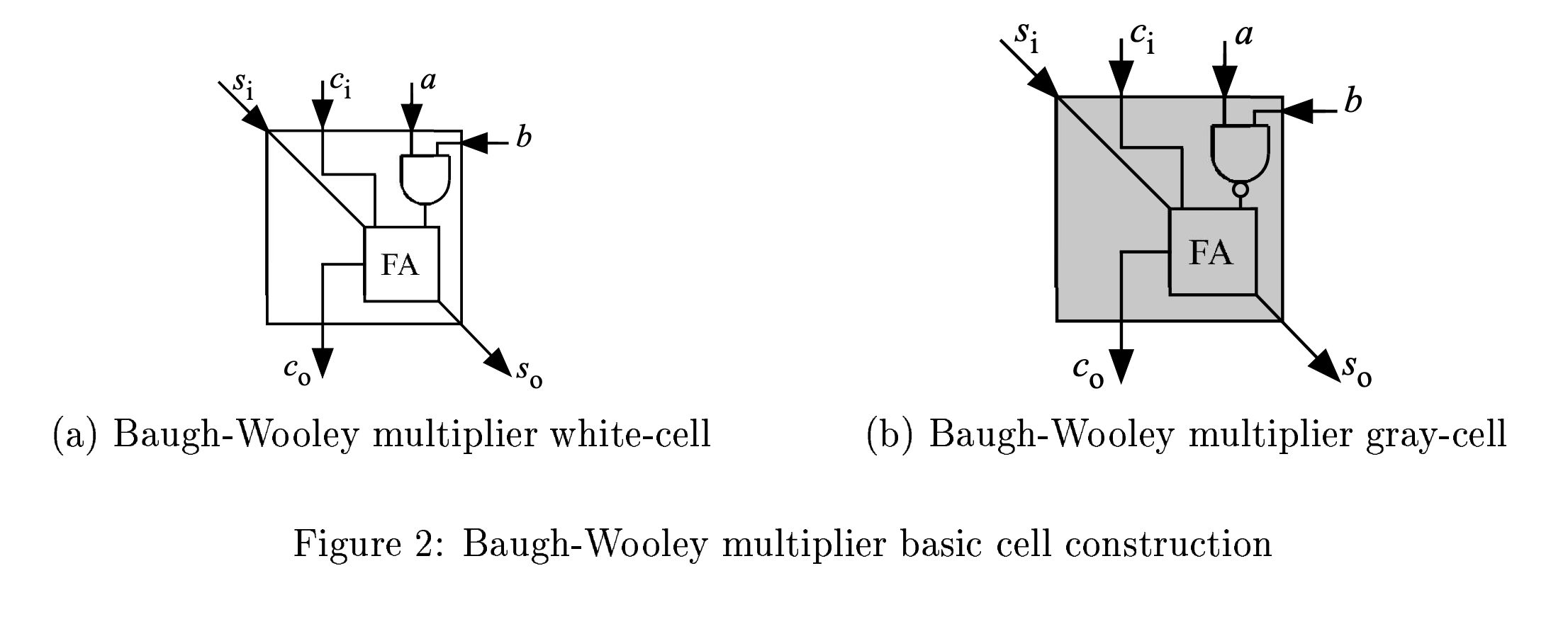
灰色與白色的運算單元差在 ab 有沒有做 complement。